Frequency, harmonics, and noise

In a spectral view, all sound is represented as a sum of frequencies with different amplitudes and phase. So if you record a pure tone (such as A4, 440Hz), you will see a straight horizontal line in the spectrogram at frequency 440 Hz. However, pure tones are typically generated by electronic devices or very specific instruments.

440 Hz sine wave

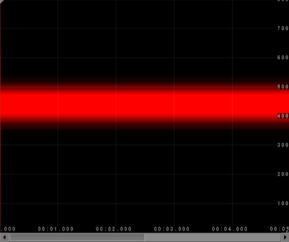
Voice and musical instruments are (mostly) composed of harmonics: several pure tones with different amplitudes and different frequencies. These frequencies follow physical rules: they are a multiple of the base frequency. If a piano plays A4, you will have a tone at 440 Hz plus a tone at 440x2=880 Hz with a different amplitude, plus a tone at 440x3=1320 Hz, etc.

Finally, noise is everything that cannot be described as pure tones. In the spectrogram, noise appears as clouds of random dots across time and frequencies.

Voice data

Voice is mostly harmonics because all vowels sounds use pure tones ("a", "e", etc). However, most consonants ("t", "k", etc) are noise. So when you select a full word you have to deal both with harmonic and noise sounds.

A voiceover recording

Instruments

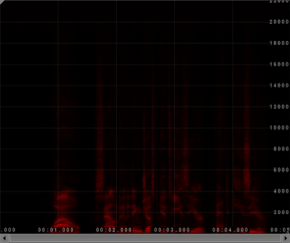
Classic instruments such as the piano, violin, trumpet, etc produce harmonic sounds.

A recorded saxophone
Some synthetic instruments may produce unharmonic sounds (harmonic-like, but with float frequency multiplier).
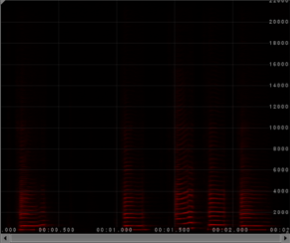
Percussive instruments such as drums produce noise.

A drum fill

Sounds from nature and engine sounds

The sea and the wind are noise.
Something that breaks or crashes is noise.
Engine sounds can be noise or harmonics.

Moving and scaling harmonics vertically

While moving or scaling noise or pure tones does not change their nature, moving harmonics breaks the harmonic rules.

Moving harmonics adds a constant frequency: if a piano plays A4 (see above) and we move this sound by 100 Hz, the 3 first frequencies will be 440+100=540 Hz, 880+100=980 Hz and 1320+100=1420 Hz.

1420 Hz and 980 Hz are not multiples of 540 Hz, which means the sound will be unharmonic (it will not sound like a piano note anymore).

To preserve the harmonics, we need to scale (multiply) the frequencies. Scaling A4 by 1.2 produces 440 x 1.2=528 Hz, 880 Hz x 1.2=1056 Hz, 1320 x 1.2=1584 Hz.

1584 Hz=528 Hz x 3 and 1056 Hz=528 Hz x 2, so we preserved harmonics and the recording will still sound like a piano.

Formant and time envelope

The formant is the frequency signature of a sound, and it applies both to harmonic and noise sounds. It is the envelope of amplitudes across frequencies.

A person's voice sounds different from another person's voice and sounds different from a piano because the harmonics are different. If they all sing and play A4, they will all have the first 3 frequencies 440 Hz, 880 Hz and 1320 Hz (see above), but with different amplitudes each. This rule also applies to noise, where the random dots are shaped by different amplitudes.

Finally the time envelope also act a signature across time. Let's take a violin: it will sound very different drawing a bow across a string or plucking it, although the frequency envelope will be the same. The way amplitudes change over time is fully part of the signature of a sound whether the sound is harmonic or noise.

If you scale a sound too much (by a factor of 2 and above, or 1/2 and below), it will not sound exactly as played by the same source, because the formant and time envelope were scaled too.

See Measuring spectral data, Positioning the cursor, Selecting spectral data and Adjusting a selection